Geodetic Dominating Set and Geodetic Domination Polynomials of Extended Grid Graphs

Abstract

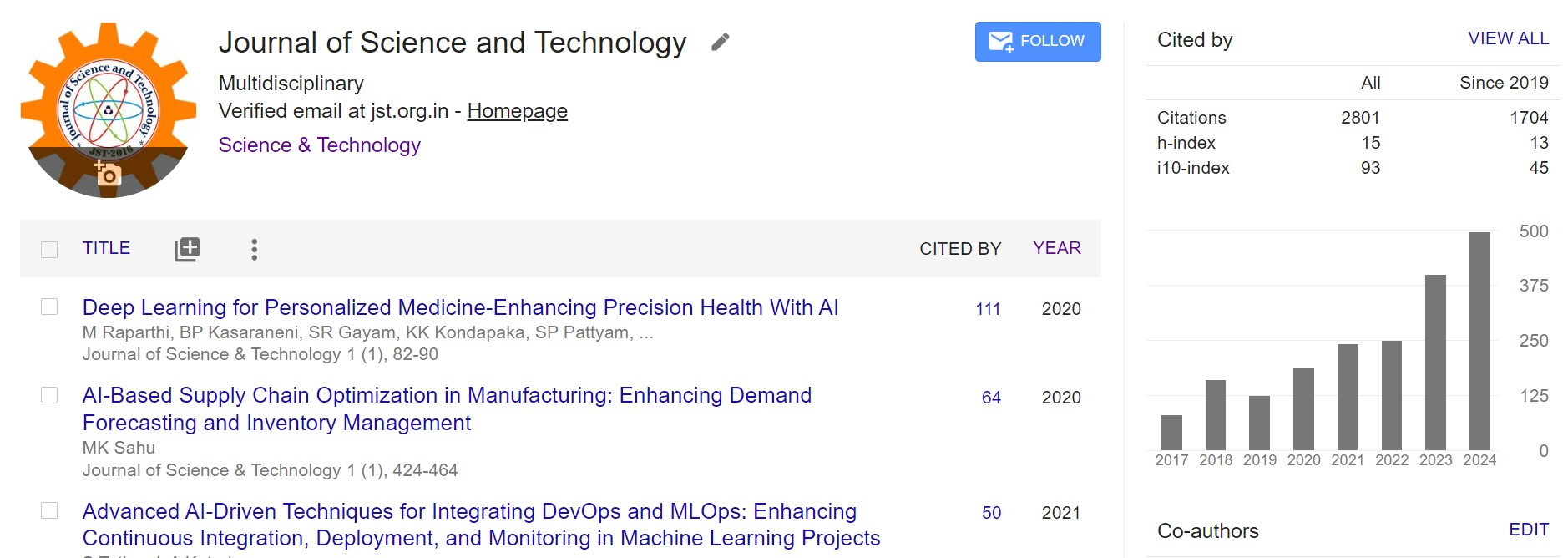
Let G = (V,E) be a simple graph. A set S  V is a dominating set of G, if every vertex in V− S is adjacent to atleast one vertex S. Let Dg(Gn, i) be the family of geodetic dominating sets of the graph Gn with cardinality 'i'. Let dg(Gn, i) = | Dg(Gn, i)|. In this paper, we obtain a recursive for dg(Gn, i). Using the recursive formula, we construct the polynomial, g(Gn) = n + 1 2     , g(Gn − {2n}) = n + 1 2     which we call geodetic dominating polynomial of Gn and obtain some properties of this polynomial.